PID-regulaatoreid kasutatakse teatavate mõõdetavate parameetrite mõjutamiseks. Nutikate 3-in-1-regulaatoritena tõestavad nad end iga päev arvukates tööstussüsteemides ja reguleerivad väga täpselt kuni seadistusväärtuseni. Anname teile kõige olulisemad faktid ja arvud PID-reguleerimise kohta.
Kompaktregulaatorit saab kohandada mitmesuguste rakenduste jaoks ja tavaliselt kasutatakse PID-regulaatorit. See töötab proportsionaalselt, integreerivalt ja diferentseerivalt (PID). Siinkohal kohandatakse üksikute komponentide intensiivsus vastavalt reguleerimisprotsessile. Seda tehakse reguleerimisparameetrite dimensioneerimise kaudu
PID-regulaatori põhimõtet on suhteliselt lihtne selgitada. Olenemata sellest, kas tegemist on PID-temperatuuriregulaatoriga või PID-niiskusregulaatoriga, püüab regulaator alati reguleerida konkreetset reguleerimismuutujat tegeliku väärtuse alusel seadistusväärtusele. Sellisel juhul võimendab P-komponent reguleerimishälvet, I-komponent suurendab olemasoleva reguleerimishälbe korral oma väljundtaset ja D-komponent tasakaalustab tegeliku väärtuse liikumist. Komponendid, mis ei ole reguleerimiseks vajalikud, saab deaktiveerida. Sõltuvalt rakendusest toimivad need siis PI-, P-, PD- või I-regulaatoritena.
PID-struktuur näitab enamiku rakenduste puhul parimat reguleerimisvastust. Seetõttu on PID-kompaktregulaatorid väga levinud temperatuuri reguleerimise valdkonnas. Need võimaldavad ka RTD-temperatuuriandurite ja termopaaride otsest ühendamist. Mõned reguleeritavad muutujad nõuavad teatavate komponentide, sealhulgas kiiruse ja voolu väljalülitamist.
P-komponent reageerib väga kiiresti ja võimendab reguleerimise erinevust; selle püsiv reguleerimishälve mõjub ebasoodsalt. Vastutav juhtimisparameeter on proportsionaalribal Pb. Kui Pb on väiksem, muutub regulaator kiiremaks ja reguleerimishälve väiksemaks. Siiski kipub kogu süsteem üha enam võnkuma.
Komponent I kõrvaldab reguleerimishälbe. Kui nullemisaeg rt on seatud väiksemaks, ehitab regulaator oma väljundtaseme kiiremini üles ja tasakaalustab ka kiiremini reguleerimishälvet. Kui aga seadistus on liiga väike, tekib samuti võnkuv käitumine.
Komponent D mõjub tegeliku väärtuse liikumisele vastu. See tähendab, et kütteregulaatori puhul vähendatakse komponenti, kui tegelik väärtus suureneb, ja suurendatakse, kui tegelik väärtus väheneb. Kirjeldatud käitumisel on summutav mõju. Vastutavaks parameetriks on tuletatud aeg dt. Mida suurem on dt, seda suurem on kirjeldatud mõju.
Reguleerimisprotsessi käitumine sõltub alati tööpunktist. Seetõttu tuleb enne häälestamist seadistada tehas sellisesse tööseisundisse, mille puhul on hiljem oodata soodsaid reguleerimisparameetreid. Näiteks tuleb enne häälestamist laadida ahju või tekitada nõudlus voolukütteseadme jaoks. Kui häälestamise ajal tuleb määrata seadepunkti väärtus, peab see jääma hilisemasse tööpiirkonda.
Kui on olemas võrreldavad seadmed/reguleerimisringid, võib neis kasutatavaid reguleerimisparameetreid kasutada katseliselt. Kui selline lähenemine ei vii eesmärgini, võib kasutada ühte järgmistest optimeerimismeetoditest.
Ziegleri ja Nichols'i kohane võnkumismeetod
Seda meetodit kasutatakse suhteliselt kiiresti kontrollitavate süsteemide puhul. Ettevalmistamiseks parameetriseeritakse P struktuur ja määratakse suhteliselt suur Pb. Järgneval joonisel on määratud järgnevas tööpiirkonnas asuv seadistusväärtus.
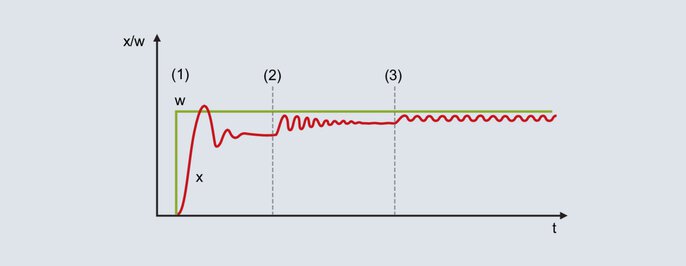
Joonis 52: Seadeväärtuse ja tegeliku väärtuse kõver võnkumismeetodi kasutamisel
Suhteliselt suureks seatud proportsionaalvahemiku korral liigub tegelik väärtus lõppväärtuse suunas, millel on väike kalduvus võnkumiseks [joonis 52 (1)]. Olematu I-struktuuri tõttu esineb püsiv reguleerimishälve.
Pb on vähendatud (joonis 52 [2]): tegelik väärtus suureneb ja liigub suurema võnkumistendentsiga lõppväärtuse suunas. Teatud tingimustel vähendatakse proportsionaalset vahemikku mitu korda, kuni tegelik väärtus on püsivalt võnkuv (joonis 52 [3]). Sellise käitumise jaoks vajalikku proportsionaalset vahemikku nimetatakse Pbc (kriitiline Pb) ja see tuleb määrata võimalikult täpselt (Pb ei tohi vähendada liiga suurte sammudega).
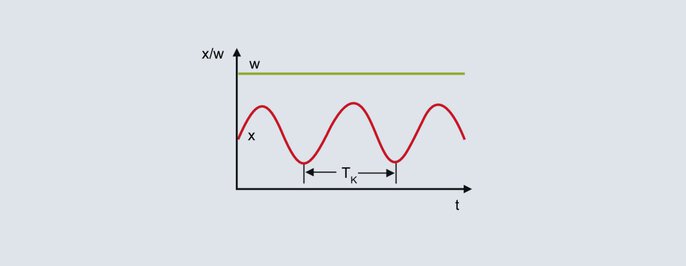
Kriitiline periood
Ülemise joonise tegeliku väärtuse pidevast võnkumisest lähtudes on kriitilise perioodi kestus Tc teine iseloomustav parameeter, mis tuleb meetodi jaoks kindlaks määrata. Kriitilise perioodi kestus Tc (sekundites) arvutatakse näiteks kahe miinimumväärtuse vahelisest ajavahemikust. Juhtimisparameetrite määramiseks sisestatakse Pbc ja Tc järgnevasse tabelisse kavandatud kontrollerstruktuuri jaoks:
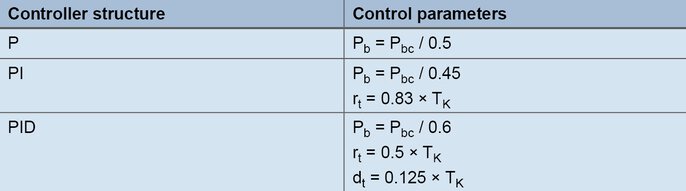
Valemid seadistamiseks vastavalt võnkumismetoodikale
Chieni, Hrones'i ja Reswicki meetod protsessietapi vastuse põhjal
Selle meetodi abil arvutatakse kontrolliparameetrid suhteliselt kiiresti, isegi aeglaste kontrolliprotsesside puhul. Meetodit kohaldatakse protsesside puhul alates teisest järjest ja seda iseloomustab asjaolu, et see eristab transientse käitumise ja häirete käitumise valemeid. Reeglite puhul arvutatakse astmelise reageeringu põhjal juhtimisprotsessi ülekandetegur, viivitusaeg ja kompensatsiooniaeg.
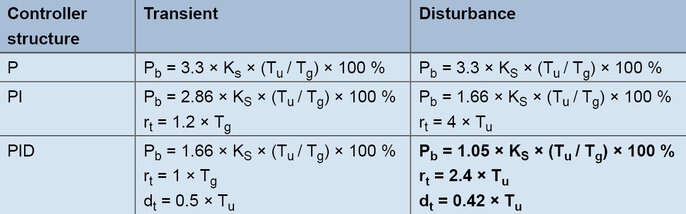
Loomisvalemid vastavalt rea sammu vastusele
Näide:
PID-struktuuriga regulaator, mida kasutatakse laboratoorses ahjus. Eesmärk on saavutada hea häirete käitumine ja tüüpilised seadistusväärtused on 200 °C. Väljunditaset suurendatakse järk-järgult käsitsi, kuni tegelik väärtus on veidi alla tulevase seadistusväärtuse (oodatakse vastavaid kompensatsiooniprotsesse). Näiteks saavutatakse temperatuur 180 °C, kui väljundtase on 60 %. Alates 60 %-st suurendatakse väljundtaset järsult 80 %ni ja tegelik väärtus registreeritakse.
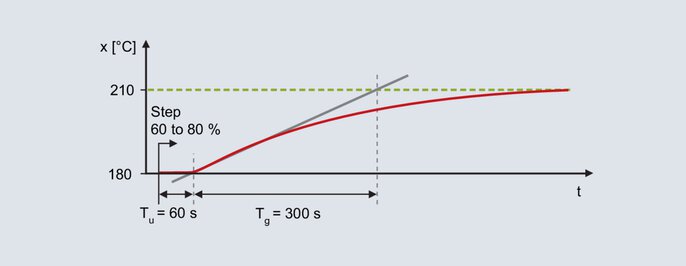
Laboratoorse ahju astmeline reaktsioon
Sammuvastuse määramine toimub paindetangendi abil: viivitusaeg Tu = 60 s, kompensatsiooniaeg Tg = 300 s. Juhtimisprotsessi ülekandetegur tuleneb tegeliku väärtuse muutusest, mis on jagatud väljundi sammuga.
Equation 22
Kasutades rusikareegleid, saadakse häire käitumise jaoks järgmised parameetrid:
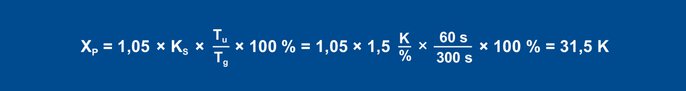
Equation 23
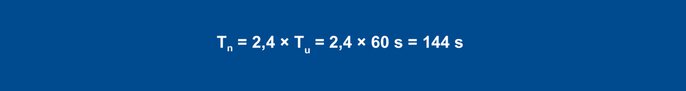
Equation 24
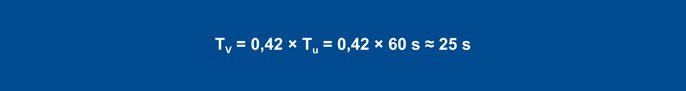
Equation 25
Väljundi samm peab toimuma järgneva tööpunkti piirkonnas. Lisaks peab sammu suurus olema seatud piisavalt suureks, et võimaldada tegeliku väärtuse kulgemise analüüsi. Kui väljundsamm on määratud, tuleb oodata tegeliku väärtuse lõppväärtust. Ajasäästev alternatiiv on meetod vastavalt tõusukiirusele.
Meetod vastavalt tõusu kiirusele
Sammu muutuse spetsifikatsiooni osas on menetlus sama, mis protsessi sammu vastuse alusel toimuva meetodi puhul. Enne astmevahetust määratakse väljundtase, mille tulemuseks on tegelik väärtus, mis on veidi väiksem kui hiljem kasutatav seadistusväärtus.
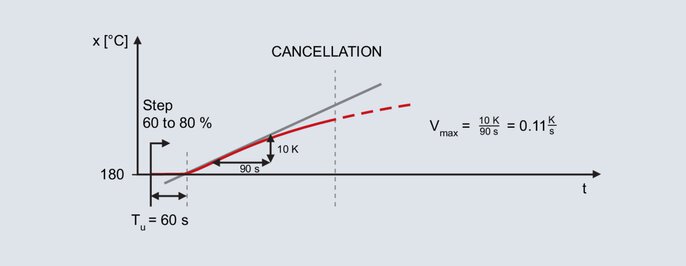
Meetodi tegeliku väärtuse kõver vastavalt pöörlemiskiirusele
Astmevahetus määratakse uuesti kindlaks juba nimetatud laboratoorsele ahjule, kusjuures järgnev töötemperatuur on samuti 200 °C. Manuaalses režiimis väljundtaseme 60 % määramine annab tegelikuks väärtuseks 180 °C. Väljundtaset suurendatakse järsku 80 %ni.
Pärast astmelise muutuse määramist suureneb tegelik väärtus mõne aja pärast. Salvestamine jätkub, kuni tegelik väärtus saavutab maksimaalse tõusu. Selle meetodiga joonistatakse ka paindetangens ja määratakse ka viivitusaeg. Teine iseloomustav parameeter on maksimaalne tõusukiirus, mis vastab paindetangendi tõusule. Maksimaalse tõusukiiruse saab määrata, rakendades paindetangendi kallakukolmnurka:
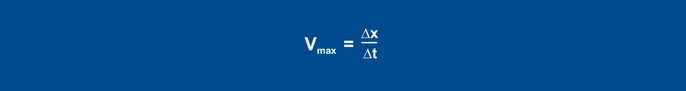
Equation 26
Arvutatud väärtusi Vmax (0,11 K/s) ja Tu (60 s) kasutatakse järgmistes valemites:
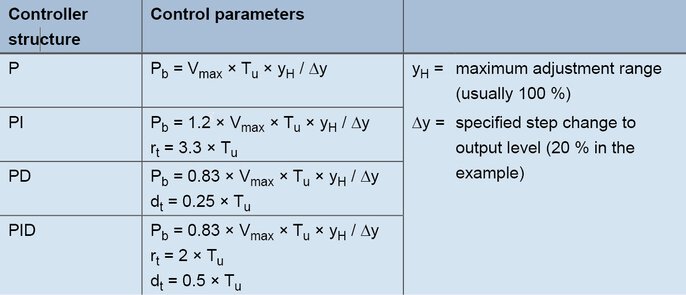
Valemid seadistamiseks vastavalt tõusukiirusele
PID-regulaatori puhul tekivad valemitega järgmised väärtused:
Equation 27
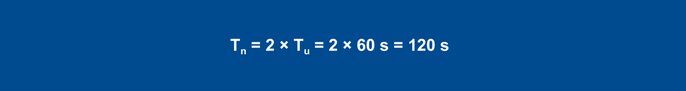
Equation 28
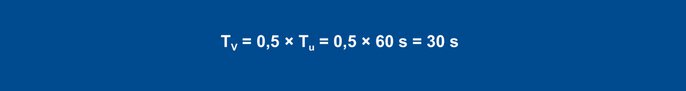
Equation 29
Empiiriline meetod kontrolliparameetrite arvutamiseks
Seda meetodit kasutatakse P-, D- ja I-komponentide optimaalsete seadete järjestikuseks arvutamiseks. Alustades algseisundist (väljundtase 0 %), määratakse iga kord tüüpiline seadistusväärtus; seetõttu sobib see meetod ainult suhteliselt kiirete reguleerimisprotsesside jaoks (näiteks kiire temperatuuri reguleerimisprotsess või sellised reguleerimismuutujad nagu kiirus või vooluhulk).
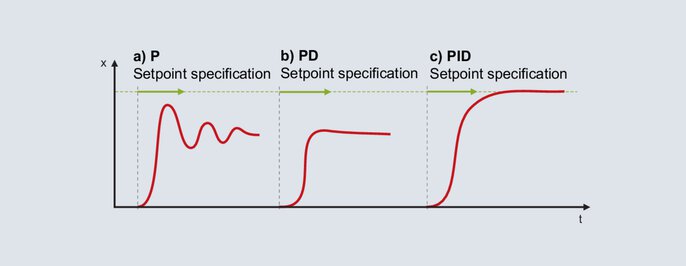
PID-regulaatori seadistamine vastavalt empiirilisele meetodile
P struktuur on kontrolleri jaoks aktiveeritud. Proportsionaalne vahemik seatakse suhteliselt suureks (dimensioneerimine sõltub reguleerimisprotsessist) ja järgnevas tööpiirkonnas määratakse seadistusväärtus. Tegelik väärtus liigub aeglaselt lõppväärtuse suunas ja tekib suhteliselt suur reguleerimishälve. Seejärel määratakse seadepunkti väärtus järjest väiksema proportsionaalvahemiku Pb abil. Eesmärk on saavutada Pb, millega tegelik väärtus saavutab stabiilse lõppväärtuse pärast 2-3 täielikku võnkumist (joonis 56a). Sujuvaks käivitamiseks tuleb struktuur lülitada P-lt PD-le. Alustades väikesest tuletusaegade seadistusest, määratakse seadepunkt üha suurema dt-ga. Kui tegelik väärtus saavutab oma lõppväärtuse võimalikult väikese võnkumise korral, on dt optimaalses seadistuses (joonis 56b).
Märkus: niipea kui regulaator seab väljundtaseme 0 %-le isegi ainult üks kord käivitamise ajal, tähendab see, et dt on seatud liiga suureks.
I-komponent aktiveeritakse, kui struktuur lülitatakse PID-ile. Optimaalne lähtestusaeg rt on üldiselt seatud 4 korda suuremaks kui eelnevalt määratud dt väärtus. Joonisel 56c on näidatud reaktsioon, kui rt = 4 × dt.
Mõne protsessi puhul ei ole võimalik kõiki komponente aktiveerida. Kui P-struktuuri puhul tekib juba suure Pb-ga ebastabiilne vastus, ei ole võimalik kasutada P- või D-struktuuri. Selle asemel tuleb kasutada I kontrollerit.
Kui P-regulaator on edukalt häälestatud, kuid D-komponendi kasutuselevõtt muudab reguleerimisskeemi ebastabiilseks, kasutatakse PI-struktuuri.
Ühe käesolevas peatükis kirjeldatud häälestusmeetodi rakendamine annab tõenäoliselt tulemuseks stabiilse, kuid mitte optimaalse reguleerimisvastuse. Reguleerimistulemust saab käsitsi ümberhäälestamisega veelgi parandada. Kui PID-regulaatori reageeringut saab sobitada ühega kõveratest 62b kuni 62e, leiate siit teavet edasiseks häälestamiseks.
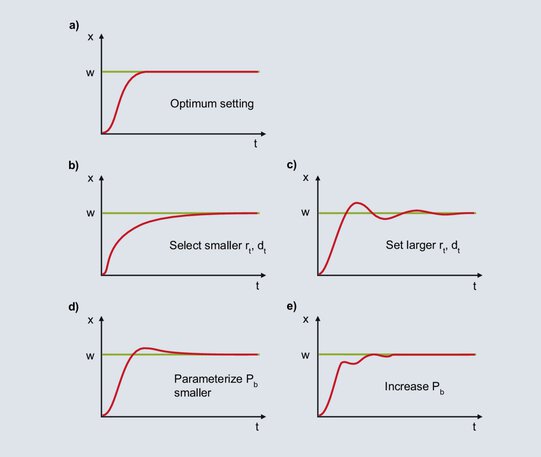
Joonis 62: Märkused PID-regulaatori järeltuunimise kohta
Diagramm näitab PID-regulaatori optimaalset käitumist.
Pärast seadistusväärtuse määramist suureneb tegelik väärtus järsult, kuni see jõuab proportsionaalpiirkonda. Kui tegelik väärtus siseneb proportsionaalsesse ribasse, vähendatakse P-komponenti ja I-komponent tagab väärtuse reguleerimise seadistusväärtusele. I-komponendi suurenemine toimub suhteliselt suure rt tõttu aeglaselt ja reguleerimishälve kõrvaldatakse aeglaselt. Kiirema integreerimise jaoks tuleb rt seada väiksemaks; dt väheneb samuti vastavalt suhtele dt/rt = 1/4.
Kui tegelik väärtus siseneb proportsionaalvööndisse, suurendab I komponent väljundtaset. Tõus jätkub, kuni tegelik väärtus jõuab seadistatud väärtuseni. Näidatud näites ehitab I-komponent ülemäärast väljundtaset kuni reguleerimishälbe kõrvaldamiseni ja tegelik väärtus ületab seadistusväärtuse. Negatiivse reguleerimishälbe korral väheneb väljundtase liiga kiiresti ja tegelik väärtus langeb alla seadistusväärtuse jne. Tegeliku väärtuse sümmeetriline võnkumine ümber seadistusväärtuse viitab liiga väikesele rt-le. rt tuleb suurendada ja dt samuti suurendada vastavalt suhtele dt / rt = 1/4.
I komponent moodustub alates hetkest, mil tegelik väärtus siseneb proportsionaalvööndisse, kuni reguleerimishälbe kõrvaldamiseni. Suure Pb tõttu hakkab I-komponent oma väljundtaset moodustama juba siis, kui on olemas suur reguleerimishälve. Alguse suure reguleerimishälbe tõttu moodustab I-komponent oma väljundtaseme suhteliselt kiiresti. Kontrollihälbe kõrvaldamisel on I-komponent liiga suur ja tegelik väärtus ületab seadistatud väärtust. Pb väiksema seadistuse korral, kui on väiksemad reguleerimishälbed, hakkab I komponent vastavalt aeglasemalt oma väljundtaset moodustama. Kirjeldatud ühekordne ületamine muutub ebatõenäolisemaks.
Liiga väikeseks seatud Pb korral väheneb P-komponendi väljundtase vahetult enne seadistusväärtuse saavutamist. Kui tegelik väärtus siseneb proportsionaalsesse vahemikku, väheneb P-komponent järsult ja tegelik väärtus väheneb. Suurema reguleerimishälbe tõttu muutub väljundtase suuremaks ja tegelik väärtus suureneb. Proportsionaalses vahemikus põhjustavad väikesed muutused tegelikus väärtuses suuri muutusi väljundtasemes, mille tulemuseks on suur kalduvus võnkumiseks. Seda rahustab proportsionaalvahemiku suurendamine.
